# Instalar o pacote lavaan (se ainda não estiver instalado)
#install.packages("lavaan")
# Carregar pacotes necessários
library(lavaan)Equações Estruturais em R: Conceitos e Aplicações Práticas
As Equações Estruturais permitem modelar relações complexas entre variáveis observadas e latentes. Elas combinam aspectos da análise fatorial e da regressão múltipla, permitindo que pesquisadores testem hipóteses sobre relações causais entre variáveis.
Neste post, vamos explorar como implementar modelos de equações estruturais em R usando o pacote lavaan. Além disso, vamos interpretar os resultados de um exemplo prático.
O que são Equações Estruturais?
Equações estruturais são modelos que permitem analisar relações entre variáveis observadas medidas diretamente (ex.: altura, idade, peso, gênero, etc.) e variáveis latentes não observadas diretamente, mas inferidas a partir de variáveis observadas. Alguns exemplos de variáveis latentes são: felicidade, ansiedade, personalidade, depressão, etc., as quais podem ser inferidas a partir de informações observadas como níveis de cortisol, interação social, consultas a psicólogos, etc. Portanto, as variáveis latentes são conceitos abstratos que não podem ser medidos diretamente.
A análise de equações estruturais é uma técnica que combina a análise de regressão múltipla e a análise fatorial para testar relações entre variáveis observáveis e latentes.
Os modelos são úteis em áreas como psicologia, ciências sociais e marketing, onde muitas vezes trabalhamos com conceitos abstratos (como “satisfação do cliente” ou “inteligência emocional”) que não podem ser medidos diretamente.
Um modelo de equações estruturais é composto por duas partes principais:
Modelo de Medida: Relaciona as variáveis observadas às variáveis latentes.
Modelo Estrutural: Define as relações entre as variáveis latentes.
Exemplo Prático: modelando a capacidade mental de crianças
O conjunto de dados de Holzinger e Swineford (1939) consiste em pontuações de testes de capacidade mental de crianças da sétima e oitava séries de duas escolas diferentes (Pasteur e Grant-White). No conjunto de dados original, há pontuações para 26 testes. No entanto, um subconjunto menor com 9 variáveis é mais amplamente usado na literatura.
Os dados são compostos por idade, sexo, escola, grade (séries), percepção visual (X1), cubos (X2), losangos (X3), compreensão de texto (X4), conclusão de frases (X5), significado das palavras (X6), soma acelerada (X7), contagem acelerada de pontos (X8), discriminação acelerada de letras maiúsculas retas e curvas (X9). As seguintes variáveis latentes podem ser usadas para inferir a capacidade mental das crianças:
Inteligência espacial: Medida por três variáveis observadas (percepção visual, cubos e losangos).
Inteligência verbal: Medida por três variáveis observadas (compreensão de texto, conclusão de frases e significado das palavras).
Velocidade: Medida por três variáveis observadas (soma acelerada, contagem acelerada de pontos e discriminação acelerada de letras maiúsculas retas e curvas).
Portanto, a capacidade mental de crianças está representada pelas variáveis latentes inteligência espacial, verbal e de velocidade, que são influenciadas pelas variáveis observadas (X1-X9). A seguir estão os passos para aplicar as análises do modelo de equações estruturais.
Passo 1: Instalar e Carregar o Pacote lavaan
Primeiro, instale e carregue o pacote lavaan, que é amplamente utilizado para modelagem de equações estruturais em R.
Passo 2: Criar o Modelo
Vamos definir o modelo de equações estruturais usando os dados HolzingerSwineford1939 do pacote lavaan. Para isso, baixamos os dados e usamos uma sintaxe específica para definir as relações entre as variáveis do modelo.
# 1. Carregar dados
data("HolzingerSwineford1939")
dados <- HolzingerSwineford1939
head(dados, 6) id sex ageyr agemo school grade x1 x2 x3 x4 x5 x6
1 1 1 13 1 Pasteur 7 3.333333 7.75 0.375 2.333333 5.75 1.2857143
2 2 2 13 7 Pasteur 7 5.333333 5.25 2.125 1.666667 3.00 1.2857143
3 3 2 13 1 Pasteur 7 4.500000 5.25 1.875 1.000000 1.75 0.4285714
4 4 1 13 2 Pasteur 7 5.333333 7.75 3.000 2.666667 4.50 2.4285714
5 5 2 12 2 Pasteur 7 4.833333 4.75 0.875 2.666667 4.00 2.5714286
6 6 2 14 1 Pasteur 7 5.333333 5.00 2.250 1.000000 3.00 0.8571429
x7 x8 x9
1 3.391304 5.75 6.361111
2 3.782609 6.25 7.916667
3 3.260870 3.90 4.416667
4 3.000000 5.30 4.861111
5 3.695652 6.30 5.916667
6 4.347826 6.65 7.500000# Criar modelo
modelo <- '
# Fatores latentes
espacial =~ x1 + x2 + x3
verbal =~ x4 + x5 + x6
velocidade =~ x7 + x8 + x9
'Aqui:
=~indica que as variáveis observadas estão associadas a uma variável latente.~indica uma relação de regressão entre variáveis latentes.
Passo 3: Ajustar o Modelo aos Dados
Vamos simular um conjunto de dados para este exemplo e ajustar o modelo. A função cfa() para ajuste do modelo significa Confimatory Factor Analysis.
# Ajustar o modelo
ajuste <- cfa(modelo, data = dados)Passo 4: Interpretar os Resultados
Use a função summary() para visualizar os resultados do modelo ajustado.
# Resumo do modelo
summary(ajuste, standardized = TRUE, fit.measures = TRUE)lavaan 0.6-19 ended normally after 35 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 21
Number of observations 301
Model Test User Model:
Test statistic 85.306
Degrees of freedom 24
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 918.852
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.931
Tucker-Lewis Index (TLI) 0.896
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3737.745
Loglikelihood unrestricted model (H1) -3695.092
Akaike (AIC) 7517.490
Bayesian (BIC) 7595.339
Sample-size adjusted Bayesian (SABIC) 7528.739
Root Mean Square Error of Approximation:
RMSEA 0.092
90 Percent confidence interval - lower 0.071
90 Percent confidence interval - upper 0.114
P-value H_0: RMSEA <= 0.050 0.001
P-value H_0: RMSEA >= 0.080 0.840
Standardized Root Mean Square Residual:
SRMR 0.065
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
espacial =~
x1 1.000 0.900 0.772
x2 0.554 0.100 5.554 0.000 0.498 0.424
x3 0.729 0.109 6.685 0.000 0.656 0.581
verbal =~
x4 1.000 0.990 0.852
x5 1.113 0.065 17.014 0.000 1.102 0.855
x6 0.926 0.055 16.703 0.000 0.917 0.838
velocidade =~
x7 1.000 0.619 0.570
x8 1.180 0.165 7.152 0.000 0.731 0.723
x9 1.082 0.151 7.155 0.000 0.670 0.665
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
espacial ~~
verbal 0.408 0.074 5.552 0.000 0.459 0.459
velocidade 0.262 0.056 4.660 0.000 0.471 0.471
verbal ~~
velocidade 0.173 0.049 3.518 0.000 0.283 0.283
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 0.549 0.114 4.833 0.000 0.549 0.404
.x2 1.134 0.102 11.146 0.000 1.134 0.821
.x3 0.844 0.091 9.317 0.000 0.844 0.662
.x4 0.371 0.048 7.779 0.000 0.371 0.275
.x5 0.446 0.058 7.642 0.000 0.446 0.269
.x6 0.356 0.043 8.277 0.000 0.356 0.298
.x7 0.799 0.081 9.823 0.000 0.799 0.676
.x8 0.488 0.074 6.573 0.000 0.488 0.477
.x9 0.566 0.071 8.003 0.000 0.566 0.558
espacial 0.809 0.145 5.564 0.000 1.000 1.000
verbal 0.979 0.112 8.737 0.000 1.000 1.000
velocidade 0.384 0.086 4.451 0.000 1.000 1.000Aqui estão alguns dos principais resultados que você verá:
Indicadores de Ajuste do Modelo:
CFI (Comparative Fit Index): Valores acima de 0.90 indicam um bom ajuste.
RMSEA (Root Mean Square Error of Approximation): Valores abaixo de 0.08 indicam um ajuste aceitável.
SRMR (Standardized Root Mean Square Residual): Valores abaixo de 0.08 são desejáveis.
Cargas Fatoriais:
- Mostram a relação entre as variáveis observadas e as variáveis latentes. Valores acima de 0.5 são considerados adequados.
Interpretação dos Resultados
Indicadores de Ajuste:
- O modelo apresenta um bom ajuste, com CFI = 0.931, RMSEA = 0.092 e SRMR = 0.065.
Cargas Fatoriais:
- Todas as cargas fatoriais são significativas (p < 0.001) e acima de 0.5, indicando que as variáveis observadas são bons indicadores das variáveis latentes.
Gerar gráfico
Passo 1: instalar pacote semPlot para criar o gráfico.
# Instale o pacote (se necessário)
#install.packages("semPlot")
# Carregue o pacote
library(semPlot)Warning: pacote 'semPlot' foi compilado no R versão 4.4.3Passo 2: Gerar o Gráfico do Modelo
# Gráfico básico do modelo
sem_plot <- semPaths(
object = ajuste,
what = "std", # Mostra coeficientes padronizados
layout = "tree", # Organização do gráfico
style = "lisrel", # Estilo visual (opcional)
sizeMan = 8, # Tamanho dos retângulos (variáveis observadas)
sizeLat = 9, # Tamanho dos círculos (variáveis latentes)
nCharNodes = 0, # Mostra nomes completos
rotation = 2, # Rotação do gráfico (2 = vertical),
color = list(
lat = "#003C30", # Cor das latentes
man = "#543005"), # Cor das observadas
edge.label.cex = 1, # Ajusta tamanho dos rótulos
label.cex = 0.8, # Tamanho dos rótulos dentro dos nós
label.color = "white",
mar = c(4, 4, 4, 4), # Margens do gráfico (variáveis observadas)
edge.width = .7, # Espessura das linhas e setas
nodeLabels = c("X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "X9","Espacial", "Verbal", "Velocidade"),
edge.color = "gray8", # Cor das linhas/setas
bg = "gray82", # Cor de fundo (cinza claro)
)
sem_plotFrom To Weight
10 --> 1 0.77
10 --> 2 0.42
10 --> 3 0.58
11 --> 4 0.85
11 --> 5 0.86
11 --> 6 0.84
12 --> 7 0.57
12 --> 8 0.72
12 --> 9 0.67
1 --> 1 0.4
2 --> 2 0.82
3 --> 3 0.66
4 --> 4 0.27
5 --> 5 0.27
6 --> 6 0.3
7 --> 7 0.68
8 --> 8 0.48
9 --> 9 0.56
10 <-> 11 0.46
10 <-> 12 0.47
11 <-> 12 0.28
11 <-> 10 0.46
12 <-> 10 0.47
12 <-> 11 0.28 Interpretação do gráfico
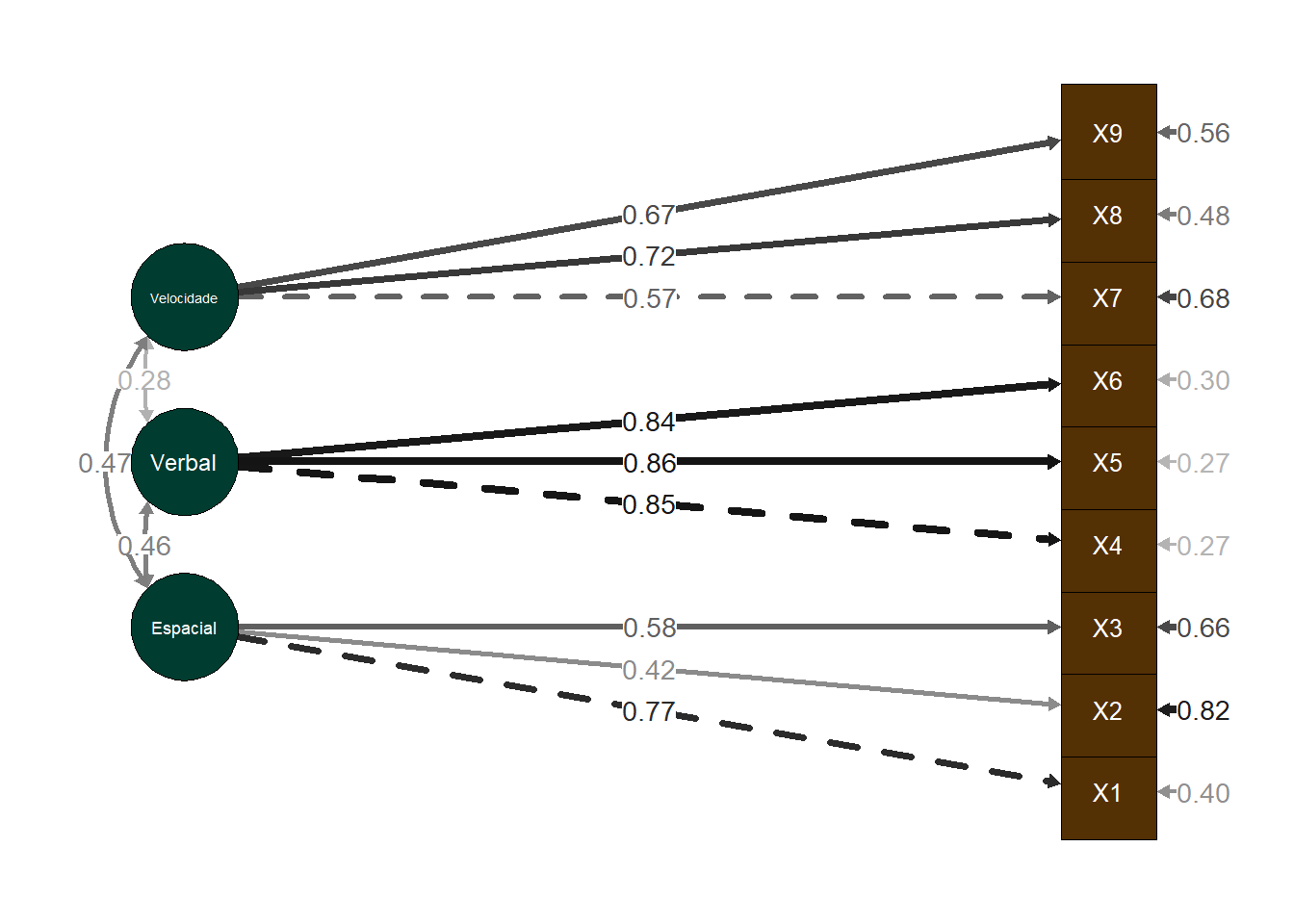
O gráfico apresenta os nós, onde estão as variáveis latentes e observadas, e as setas indicam as relações entre elas. As variáveis apresentadas nos círculos (Espacial, Verbal, Velocidade) são as variáveis latentes influenciadas pelas variáveis observadas percepção visual (X1), cubos (X2), losangos (X3), compreensão de texto (X4), conclusão de frases (X5), significado das palavras (X6), soma acelerada (X7), contagem acelerada de pontos (X8), discriminação acelerada de letras maiúsculas retas e curvas (X9) apresentadas nos quadrados. Os valores atrelados às setas são as estimativas padronizadas de caminhos, indicadas no resumo dos resultados pelos std.all. As estimativas das relações entre as variáveis latentes indicam as covariâncias e as estimativas sobre as variáveis observadas são as suas variâncias, como indicado na tabela também pelos valores std.all. As setas indicam relações unidirecionais entre as variáveis, quando uma tem influência sobre a outra. Setas tracejadas indicam caminhos não diretos ou residuais e setas sólidas indicam relações diretas entre as variáveis. Setas mais escuras indicam relações mais fortes entre as variáveis, de acordo com a estimativa padronizada, e setas mais claras indicam relações mais fracas.
Conclusão
Neste post, exploramos como implementar e interpretar modelos de equações estruturais em R usando o pacote lavaan. Essa técnica é poderosa para testar hipóteses complexas e entender relações entre variáveis latentes e observadas.
Se você tiver dúvidas ou quiser explorar mais sobre o tema, deixe um comentário abaixo! E não se esqueça de compartilhar este post com seus colegas que também se interessam por programação em R e análise de dados.