ANOVA Two-Way

Códigos
ANOVA
estatística
Autor

Jeanne Franco

Data de Publicação

25 de abril de 2025

ANOVA Two-Way no R: Introdução e Exemplo Prático

O que é ANOVA Two-Way?

A ANOVA de dois fatores (two-way ANOVA) é uma técnica estatística usada para analisar os efeitos de dois fatores categóricos (variáveis independentes) sobre uma variável contínua (variável dependente). Além disso, ela permite verificar se existe interação entre os dois fatores.

Hipóteses da ANOVA Two-Way

  1. Efeito do Fator A:

H₀: Não há diferença entre os grupos do Fator A.

H₁: Pelo menos um grupo do Fator A difere dos outros.

  1. Efeito do Fator B:

H₀: Não há diferença entre os grupos do Fator B.

H₁: Pelo menos um grupo do Fator B difere dos outros.

  1. Interação entre Fator A e Fator B:

H₀: Não há interação entre os fatores.

H₁: Existe interação entre os fatores.

Exemplo prático no R

Vamos usar o conjunto de dados ToothGrowth, que já vem com o R. Ele contém informações sobre o crescimento de dentes de 60 porquinhos-da-índia em função de dois fatores:

  • supp (suplemento: VC = vitamina C, OJ = suco de laranja).

  • dose (dose de vitamina C: 0.5, 1, 2 mg/dia).

  • len (comprimento dos odontoblastos (células responsáveis pelo crescimento dos dentes)

Passo 1: Carregar os pacotes, o conjunto de dados ToothGrowth e explorar

# Carregar pacote

library(ggplot2) # Gráficos
library(tidyverse) # Estrutura dos dados

# Carregar dados

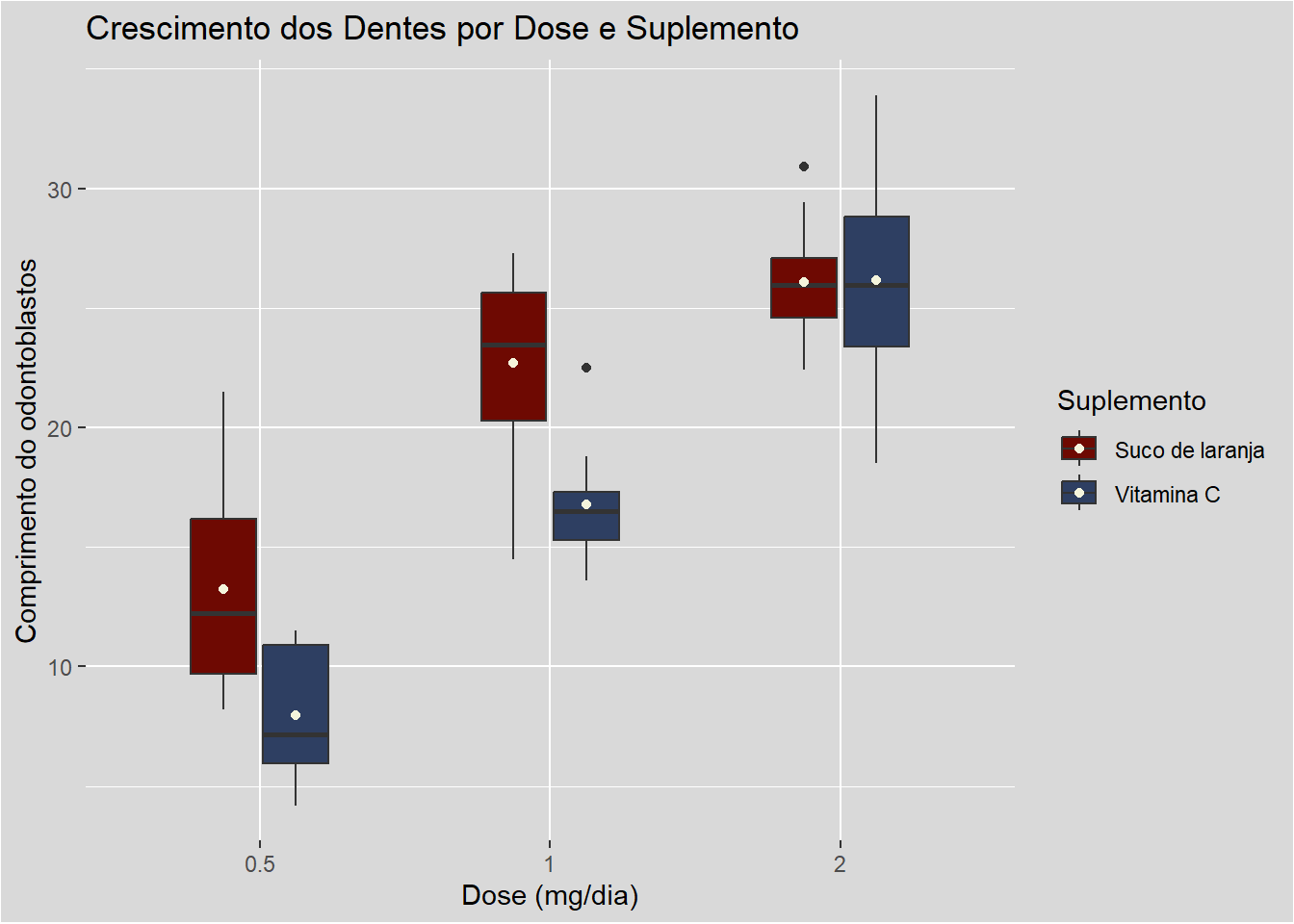
data("ToothGrowth")
head(ToothGrowth)
   len supp dose
1  4.2   VC  0.5
2 11.5   VC  0.5
3  7.3   VC  0.5
4  5.8   VC  0.5
5  6.4   VC  0.5
6 10.0   VC  0.5
# Resumo estatístico

summary(ToothGrowth)
      len        supp         dose      
 Min.   : 4.20   OJ:30   Min.   :0.500  
 1st Qu.:13.07   VC:30   1st Qu.:0.500  
 Median :19.25           Median :1.000  
 Mean   :18.81           Mean   :1.167  
 3rd Qu.:25.27           3rd Qu.:2.000  
 Max.   :33.90           Max.   :2.000  
# Verificar estrutura

glimpse(ToothGrowth)
Rows: 60
Columns: 3
$ len  <dbl> 4.2, 11.5, 7.3, 5.8, 6.4, 10.0, 11.2, 11.2, 5.2, 7.0, 16.5, 16.5,…
$ supp <fct> VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, V…
$ dose <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0, 1.0, 1.0, …

Passo 2: Visualizar os dados

Vamos usar o ggplot2 para criar um boxplot e ver a distribuição:

ggplot(ToothGrowth, aes(x = factor(dose), 
                        y = len, fill = supp)) +
  geom_boxplot(width = 0.5) +
  labs(title = "Crescimento dos Dentes por Dose e Suplemento",
       x = "Dose (mg/dia)", y = "Comprimento do odontoblastos") +
 stat_summary(fun.y = "mean", geom = "point", size = 1.5,
    position = position_dodge(width = 0.5), color = "beige") +
  scale_fill_manual(values = c("#6E0902", "#2E3F62"),
                    name = "Suplemento",
                    breaks = c("OJ", "VC"),
                    labels = c("Suco de laranja", "Vitamina C")) +
  scale_color_manual(values = c("#6E0902", "#2E3F62")) +
  theme(plot.background = element_rect(fill = "gray85"),
        panel.background = element_rect(fill = "gray85"),
        legend.background = element_rect(fill = "gray85"))

Passo 3: Pressupostos da ANOVA Two-Way

Antes de interpretar a ANOVA two-way, sempre verifique os pressupostos. No exemplo do ToothGrowth, se os resíduos forem normais e as variâncias homogêneas, a análise é válida. Caso contrário, considere transformações ou métodos alternativos.

  1. Normalidade dos resíduos:

    • Os resíduos do modelo devem seguir uma distribuição normal.

    • Verificação: Teste de Shapiro-Wilk ou gráficos Q-Q.

  2. Homogeneidade das variâncias (homocedasticidade):

    • As variâncias dos grupos devem ser aproximadamente iguais.

    • Verificação: Teste de Levene ou Bartlett.

  3. Independência das observações:

    • As amostras devem ser independentes (geralmente garantido pelo desenho experimental).

    Exemplo de Código Completo com Verificação de Pressupostos

# Passo 1: ANOVA Two-Way

modelo_anova <- aov(len ~ supp * factor(dose), data = ToothGrowth)

summary(modelo_anova)
                  Df Sum Sq Mean Sq F value   Pr(>F)    
supp               1  205.4   205.4  15.572 0.000231 ***
factor(dose)       2 2426.4  1213.2  92.000  < 2e-16 ***
supp:factor(dose)  2  108.3    54.2   4.107 0.021860 *  
Residuals         54  712.1    13.2                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Passo 2: Verificar normalidade

shapiro.test(residuals(modelo_anova))

    Shapiro-Wilk normality test

data:  residuals(modelo_anova)
W = 0.98499, p-value = 0.6694
qqnorm(residuals(modelo_anova))
qqline(residuals(modelo_anova), col = "red")

# Passo 3: Verificar homogeneidade de variâncias

library(car)

leveneTest(len ~ supp * factor(dose), data = ToothGrowth)
Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  5  1.7086 0.1484
      54

O que fazer se os pressupostos não forem atendidos?

  1. Se não houver normalidade:

    • Transformar a variável dependente (log, sqrt).

    • Usar um teste não paramétrico (ex: Teste de Kruskal-Wallis para dois fatores).

  2. Se não houver homogeneidade de variâncias:

    • Usar correções como ANOVA com ajuste de Welch (oneway.test()).
    • Aplicar transformações nos dados.

Passo 4: Realizar a ANOVA Two-Way

Usaremos a função aov():

# Ajustar o modelo ANOVA

modelo_anova <- aov(len ~ supp * factor(dose), data = ToothGrowth)

# Ver os resultados

summary(modelo_anova)
                  Df Sum Sq Mean Sq F value   Pr(>F)    
supp               1  205.4   205.4  15.572 0.000231 ***
factor(dose)       2 2426.4  1213.2  92.000  < 2e-16 ***
supp:factor(dose)  2  108.3    54.2   4.107 0.021860 *  
Residuals         54  712.1    13.2                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Passo 5: Teste Post-Hoc (se necessário)

Se a ANOVA for significativa, podemos usar o Tukey HSD para comparações múltiplas:

TukeyHSD(modelo_anova)
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = len ~ supp * factor(dose), data = ToothGrowth)

$supp
      diff       lwr       upr     p adj
VC-OJ -3.7 -5.579828 -1.820172 0.0002312

$`factor(dose)`
        diff       lwr       upr   p adj
1-0.5  9.130  6.362488 11.897512 0.0e+00
2-0.5 15.495 12.727488 18.262512 0.0e+00
2-1    6.365  3.597488  9.132512 2.7e-06

$`supp:factor(dose)`
               diff        lwr        upr     p adj
VC:0.5-OJ:0.5 -5.25 -10.048124 -0.4518762 0.0242521
OJ:1-OJ:0.5    9.47   4.671876 14.2681238 0.0000046
VC:1-OJ:0.5    3.54  -1.258124  8.3381238 0.2640208
OJ:2-OJ:0.5   12.83   8.031876 17.6281238 0.0000000
VC:2-OJ:0.5   12.91   8.111876 17.7081238 0.0000000
OJ:1-VC:0.5   14.72   9.921876 19.5181238 0.0000000
VC:1-VC:0.5    8.79   3.991876 13.5881238 0.0000210
OJ:2-VC:0.5   18.08  13.281876 22.8781238 0.0000000
VC:2-VC:0.5   18.16  13.361876 22.9581238 0.0000000
VC:1-OJ:1     -5.93 -10.728124 -1.1318762 0.0073930
OJ:2-OJ:1      3.36  -1.438124  8.1581238 0.3187361
VC:2-OJ:1      3.44  -1.358124  8.2381238 0.2936430
OJ:2-VC:1      9.29   4.491876 14.0881238 0.0000069
VC:2-VC:1      9.37   4.571876 14.1681238 0.0000058
VC:2-OJ:2      0.08  -4.718124  4.8781238 1.0000000

Interpretação dos Resultados

Como observado nos valores de p ANOVA two-way e no gráfico, ocorreu efeito significativo tanto do suplemento supp como efeito da dose dose e das suas interações supp:factor(dose).