GLMM combina duas abordagens poderosas:
GLM (Modelos Lineares Generalizados): Extensão de modelos lineares para respostas não-normais (binárias, Poisson, etc.). Isso ocorre quando as variáveis resposta não seguem a distribuição normal, muitas vezes essas variáveis podem representar dados de contagem, dados binários, porcentagens, etc., seguindo, portanto, outras distribuições.
Efeitos aleatórios: Incorpora variação hierárquica ou agrupamento nos dados (ex.: medidas repetidas, dados aninhados). Esses efeitos aleatórios são incluídos quando os grupos apresentam dependência entre as observações dentre de um mesmo grupo, por exemplo, medidas do crescimento de plantas ao longo do tempo em uma mesma planta, ou quando cada sujeito em um grupo avaliado apresenta diferentes características, por exemplo, alunos de uma escola, parcelas em um experimento de floresta, pacientes de um hospital, etc.
Quando seus dados têm estrutura hierárquica (ex.: alunos em escolas, repetições no tempo).
Quando a variável resposta não é contínua/normal (ex.: contagens, proporções, binária).
Use o ICC (Coeficiente de Correlação Intraclasse) do pacote performance para medir a similaridade dentro dos grupos. Valores próximos de 1 indicam forte hierarquia. Veja o código abaixo de como fazer isso:
performance::icc(modelo_glmm)Como exemplo, vamos utilizar o conjunto de dados sleepstudy presente em um pacote do R. Esses dados tratam de um teste de cognição, do tempo médio de reação (em milissegundos) para indivíduos em um estudo de privação do sono.
O conjunto de dados sleepstudy apresenta 180 observações e as seguintes 3 variáveis:
Reaction: tempo médio de reação (ms);
Days: número de dias de privação de sono;
Subject: número do indivíduo em que as observações foram feitas.
Agora, vamos a prática no R:
# Pacotes
library(lme4) # Para GLMM
library(ggplot2) # Para gráficos
library(NatParksPalettes) # Seleção de cores para os gráficos
# Dados
data("sleepstudy")
head(sleepstudy) Reaction Days Subject
1 249.5600 0 308
2 258.7047 1 308
3 250.8006 2 308
4 321.4398 3 308
5 356.8519 4 308
6 414.6901 5 308ggplot(sleepstudy, aes(x = Days, y = Reaction, color = Subject)) +
geom_point(size = 2.2) +
geom_smooth(method = "lm", se = FALSE, size = 1) +
scale_color_manual(values = natparks.pals("Triglav", 18)) +
theme(plot.background = element_rect(fill = "gray85"),
panel.background = element_rect(fill = "gray85"),
legend.background = element_rect(fill = "gray85")) +
labs(title = "Tempo de Reação por Dia (por Indivíduo)",
x = "Dias de Privação de Sono",
y = "Tempo de Reação (ms)",
color = "Indivíduos") +
guides(colour = guide_legend(ncol = 2))
Observação: Há variação entre indivíduos (efeito aleatório), mas um padrão geral de aumento do tempo de reação com mais dias de privação (efeito fixo).
Suponha que Reaction siga uma distribuição Gamma (para ilustrar GLMM não-normal). Usaremos:
Efeito fixo: Days (dias de privação).
Efeito aleatório: Intercepto por Subject (variação individual).
modelo_glmm <- glmer(Reaction ~ Days + (1 | Subject),
family = Gamma(link = "log"),
data = sleepstudy)
# Resumo do modelo
summary(modelo_glmm)Generalized linear mixed model fit by maximum likelihood (Laplace
Approximation) [glmerMod]
Family: Gamma ( log )
Formula: Reaction ~ Days + (1 | Subject)
Data: sleepstudy
AIC BIC logLik deviance df.resid
1748.8 1761.6 -870.4 1740.8 176
Scaled residuals:
Min 1Q Median 3Q Max
-2.6824 -0.5786 0.0493 0.5532 3.9858
Random effects:
Groups Name Variance Std.Dev.
Subject (Intercept) 0.005767 0.07594
Residual 0.011111 0.10541
Number of obs: 180, groups: Subject, 18
Fixed effects:
Estimate Std. Error t value Pr(>|z|)
(Intercept) 5.531748 0.043862 126.1 <2e-16 ***
Days 0.033809 0.002523 13.4 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
Days -0.252
optimizer (Nelder_Mead) convergence code: 0 (OK)
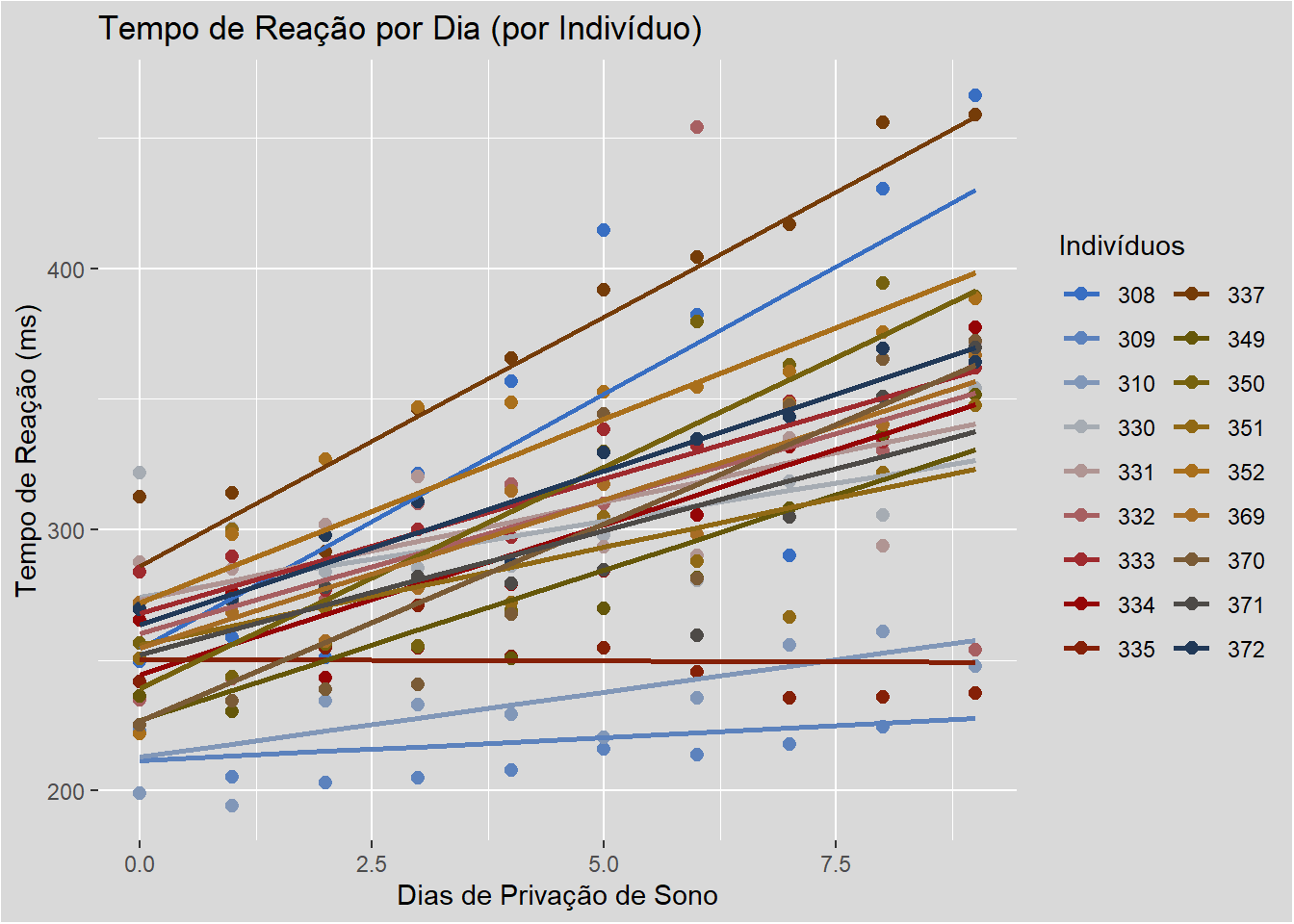
Model failed to converge with max|grad| = 0.00217371 (tol = 0.002, component 1)Interpretação da tabela:
Efeito fixo (Days): Coeficiente positivo indica aumento no tempo de reação com mais dias (valor de p significativo).
Efeito aleatório (Subject): Variância do intercepto mostra diferenças entre indivíduos.
sleepstudy$pred <- predict(modelo_glmm, type = "response")
ggplot(sleepstudy, aes(x = Days, y = Reaction, color = Subject)) +
geom_point(size = 2.2) +
geom_line(aes(y = pred, group = Subject), size = 1) +
scale_color_manual(values = natparks.pals("Triglav", 18)) +
theme(plot.background = element_rect(fill = "gray85"),
panel.background = element_rect(fill = "gray85"),
legend.background = element_rect(fill = "gray85")) +
labs(title = "Tempo de Reação por Dia (por Indivíduo)",
x = "Dias de Privação de Sono",
y = "Tempo de Reação (ms)",
color = "Indivíduos") +
guides(colour = guide_legend(ncol = 2))
Checagem do Modelo: Use DHARMa para diagnósticos de resíduos.
Outros Distribuições: Troque Gamma por poisson ou binomial conforme seus dados. Dados inteiros como os de contagem costumam apresentar distribuição do tipo poisson e dados binários apresentam distribuição do tipo binomial.
DHARMalibrary(DHARMa)
simulacoes <- simulateResiduals(modelo_glmm, n = 1000) # Simula 1000 conjuntos de dados
plot(simulacoes) # Gera 4 gráficos de diagnóstico
Como verificado no diagnóstico, o modelo não se ajustou bem aos dados sleepstudy, portanto, devemos adequar o modelo para uma análise mais confiável.
Como é possível que o efeito de dias Days varie entre indivíduos, então podemos adicionar mais uma variação aleatória de dias. Também vamos utilizar a função alternativa glmmTMB para permitir melhor ajuste.
O glmmTMB é um pacote do R que surgiu como uma alternativa mais flexível e robusta ao lme4 para ajustar GLMMs (Modelos Lineares Generalizados Mistos).
Enquanto lme4 suporta apenas algumas distribuições (Gaussiana, Binomial, Poisson), o glmmTMB inclui opções como:
Beta: Para proporções contínuas (ex.: 0 < y < 1).
Tweedie: Para dados contínuos com excesso de zeros.
Nbinom2 (Binomial Negativa): Para contagens superdispersas.
Gamma, Log-Normal, etc.
# Carregar pacote glmmTMB
library(glmmTMB)
# Gerar modelo
modelo_glmmTMB <- glmmTMB(Reaction ~ Days + (1 + Days | Subject),
family = gaussian(),
data = sleepstudy)
# Carregar pacote DHARMa para realizar diagnóstico
library(DHARMa)
# Diagnóstico final
simulacoes_final <- simulateResiduals(modelo_glmmTMB)
plot(simulacoes_final)
# Resumo do modelo
summary(modelo_glmmTMB) Family: gaussian ( identity )
Formula: Reaction ~ Days + (1 + Days | Subject)
Data: sleepstudy
AIC BIC logLik deviance df.resid
1763.9 1783.1 -876.0 1751.9 174
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
Subject (Intercept) 565.49 23.780
Days 32.68 5.717 0.08
Residual 654.94 25.592
Number of obs: 180, groups: Subject, 18
Dispersion estimate for gaussian family (sigma^2): 655
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 251.404 6.632 37.91 < 2e-16 ***
Days 10.467 1.502 6.97 3.22e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Agora, verificamos um bom ajuste do modelo, usando dias e indivíduos como variáveis aleatórias.
sleepstudy$pred1 <- predict(modelo_glmmTMB, type = "response")
ggplot(sleepstudy, aes(x = Days, y = Reaction, color = Subject)) +
geom_point(aes(color = Subject), size = 2.2) +
geom_line(aes(y = pred1, group = Subject), size = 1) +
scale_color_manual(values = natparks.pals("Triglav", 18)) +
theme(plot.background = element_rect(fill = "gray85"),
panel.background = element_rect(fill = "gray85"),
legend.background = element_rect(fill = "gray85")) +
labs(title = "Tempo de Reação por Dia (por Indivíduo)",
x = "Dias de Privação de Sono",
y = "Tempo de Reação (ms)",
color = "Indivíduos") +
guides(colour = guide_legend(ncol = 2))
Calcular o R² (coeficiente de determinação) para modelos GLMM (como os ajustados com lme4 ou glmmTMB) não é tão direto quanto em modelos lineares tradicionais (LM), pois esses modelos incorporam efeitos aleatórios e podem usar distribuições não-normais.
Há duas versões principais, conforme propostas por Nakagawa & Schielzeth (2013):
R² marginal (R2m): Explica a variância pelos efeitos fixos (ex.: Days no sleepstudy).
R² condicional R2c): Inclui efeitos fixos + aleatórios (ex.: Subject).
performanceA maneira mais simples é usar a função r2() do pacote performance (que funciona com lme4, glmmTMB, brms, etc.):
# Pacote para calcular o R²
library(performance)
# Calcular R² marginal e condicional
r2 <- r2(modelo_glmmTMB)
print(r2)# R2 for Mixed Models
Conditional R2: 0.793
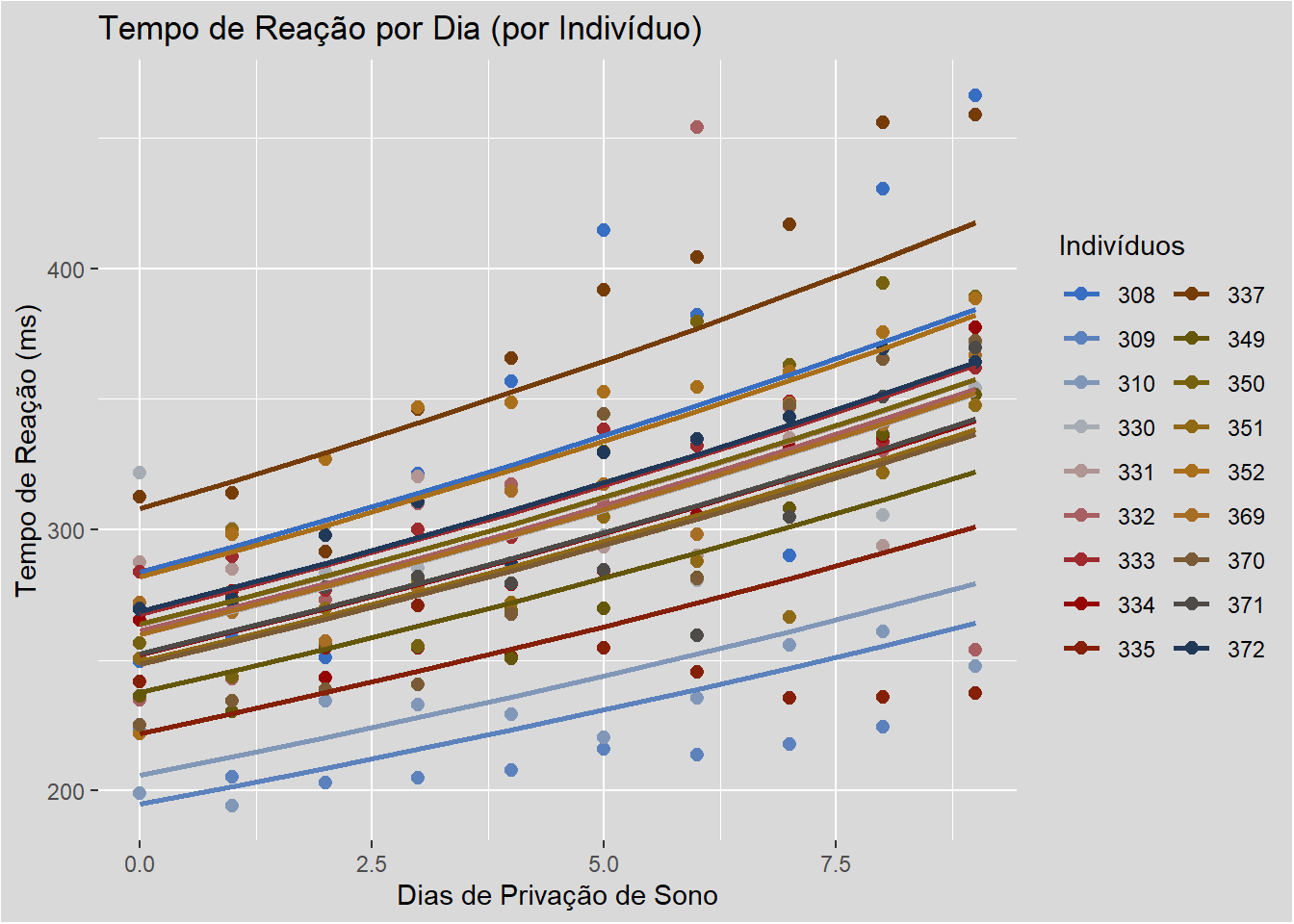
Marginal R2: 0.288R² marginal = 0.288: Apenas 28.8% da variância em Reaction é explicada por Days (efeito fixo).
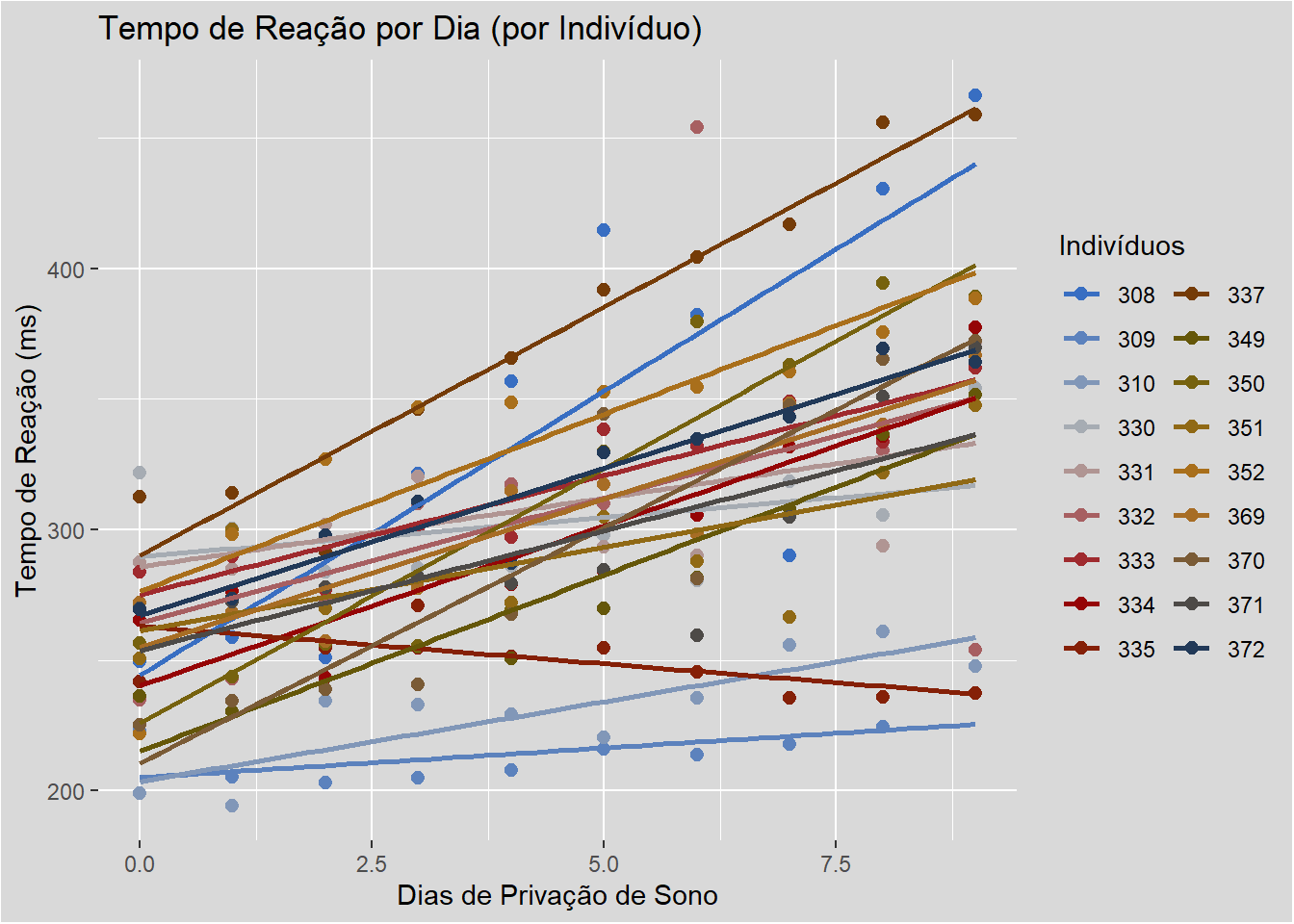
R² condicional =0.793: 79.3% da variância é explicada por Days + diferenças individuais entre Subject (efeitos aleatórios).
Quanto maior a diferença entre o R² marginal e o R² condicional, mais importante são os efeitos aleatórios no modelo.
Os efeitos aleatórios em modelos mistos (GLMMs) capturam variações não explicadas pelos efeitos fixos, mas que estão associadas a estruturas hierárquicas ou agrupamentos nos dados (ex.: indivíduos, parcelas, tempo).
A grande diferença (0.79−0.28=0.51) indica que os efeitos aleatórios dominam a explicação do modelo. Ou seja, as características individuais dos sujeitos importam mais que o efeito geral dos dias.
Se os efeitos aleatórios dominam (R² condicional muito maior que R² marginal), isso sugere que:
Sua pergunta científica deve focar nos grupos (ex.: “Por que alguns indivíduos são mais afetados?”).
Você pode precisar de mais covariáveis para explicar as diferenças entre grupos.
Portanto, se o R² condicional do seu modelo GLMM for significativamente maior que o R² marginal, isso sugere que outras variáveis não medidas — como hábitos individuais (alimentação, medicamentos, atividade física) ou características intrínsecas (genética, metabolismo) — podem estar influenciando o tempo de reação.
Isso indica que cerca de 50% da variância restante (0.79−0.28) vem de fatores não controlados, como:
Hábitos de vida (caféina, exercícios).
Uso de medicamentos (estimulantes, antidepressivos).
Condições de saúde (estresse, qualidade do sono basal).
Suponha que:
Alimentação: Pessoas com dieta rica em ômega-3 têm tempos de reação menores.
Café: Consumo diário reduz o efeito da privação de sono.
Se essas variáveis não forem medidas, seu modelo atribuirá essa variação aos efeitos aleatórios (Subject), inflando o R² condicional. Considerando isso, é necessário reconhecer as limitações das análises, pois diferenças entre indivíduos não medidas explicam parte dos resultados, e sugerir novos estudos adicionando ao modelo dados sobre hábitos de vida.
GLMM é essencial para dados com estrutura complexa e não-normais. No exemplo, modelamos a relação entre privação de sono e tempo de reação, considerando diferenças individuais.